
No, mutant Y does not genetically complement mutant Z. Gravitated toward experiments that provide clear-cut “yes” or “no” types of answers. In fact, reading this statement today, many of us might well identify with this point of view. We also address issues related to sample size, normality, outliers, and non-parametric approaches.Īt the first group meeting that I attended as a new worm postdoc (1997, D.S.F.), I heard the following opinion expressed byĪ senior scientist in the field: “If I need to rely on statistics to prove my point, then I'm not doing the right experiment.” Our chapter includes a description of basic terms and centralĬoncepts and also contains in-depth discussions on the analysis of means, proportions, ratios, probabilities, and correlations. Use common examples as illustrations for statistical analysis. Our intent has been to limit theoretical considerations to a necessary minimum and to Although the majority of examples are drawn from theįield of Caenorhabditis elegans biology, the concepts and practical applications are also relevant to those who work in the disciplines of molecular geneticsĪnd cell and developmental biology. This methods chapter is written with such individuals in mind. Many researchers who are otherwise rigorous and thoughtful in their scientific approach lack sufficient knowledge of thisįield. Level of designing one's own experiments as well as for critically evaluating studies carried out by others. The proper understanding and use of statistical tools are essential to the scientific enterprise. Appendix D: Useful websites for statistical calculations Appendix C: Useful programs for statistical calculations 12. Additional considerations and guidelines 6.1. Ratio of means versus mean of ratios 5.3. Comparing relative versus incremental differences 5.2. Relative differences, ratios, and correlations 5.1. Tests for differences between multinomial proportions 5. Probability calculations when sample sizes are large relative to the population size 4.13. Probability calculations for binomial proportions 4.12. Tests for differences between more than one binomial proportion 4.11. Tests for differences between two binomial proportions 4.10.
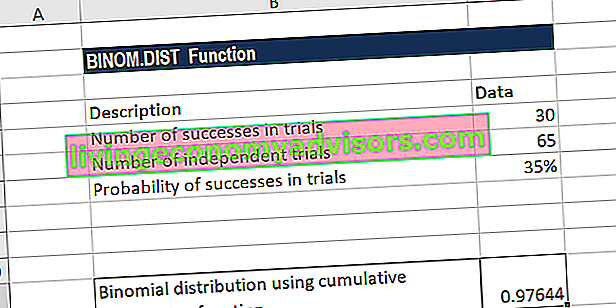
Calculating confidence intervals for binomial proportions 4.9. Conditional probability: calculating probabilities when events are not independent 4.7. Intuitive methods for calculating probabilities 4.6. Calculating more-complex probabilities 4.4.
A philosophical argument for making no adjustments for multiple comparisons 4. When are multiple comparison adjustments not required? 3.9. Summary of multiple comparisons methods 3.8. Is there a minimum acceptable sample size? 2.8. Understanding the t-test: a brief foray into some statistical theory 2.3. A quick guide to interpreting different indicators of variation 1.7. What is the best way to report variation in data? 1.6. Quantifying variation in population or sample data 1.3.


 0 kommentar(er)
0 kommentar(er)
